English homepage Japanese homepage Contents
Eddington first took notice of Whitehead's theory. He proved in his 1924 paper that Whitehead's equation has the same solution (the Schwartzchild solution) as Einstein's in the special case of the stationary gravitational field due to a single mass-point.16 The implication of this equivalence was that Whitehead's theory can pass the standard tests such as periherion precession of Mercury and the bending of light-rays close to the sun. The similar result was obtained by Temple, who also gave a generalized version of Whitehead's theory which holds in the space-time with constant curvature.17 In the 1920s, the comparison of two theories was mainly on the level of conceptual analysis, for both gave the same results under the limited conditions, and it was difficult to choose between them on experimental grounds then available. The question at issue was the justifiability of Whitehead's theory which, presupposing Minkowski's space globally, rejected the general principle of relativity. For example, Band criticized Whitehead by pointing out that the acceptance of a uniform or "fiat" space was untenable on account of the illegitimate assumption of a standard of absolutely uniform motion.18 But the problem of finding the exact solutions of both theory other than Schwartzchild's was so difficult that the crucial experiment between them was not yet contrived.
In the 1930s and 1940s the main interests of physicists shifted to the realm of quantum mechanics and nuclear physics which developed without relying on any gravitational theory. Here physicists were satisfied only with the special theory of relativity, and kept away from Einstein's later project of relativistic cosmology and the unified theory of fields. Whitehead was regarded as a metaphysician, and his theory of relativity seemed to be virtually ignored during this period. The re-evaluation of Whitehead's theory began in the 1950s, which was due to an Irish physicist, Synge, who esteemed Whitehead's theory for its elegance and originality, and located it between Newton's theory of action-at-a-distance, and Einstein's theory of local action. Setting aside Whitehead's philosophical background, Synge reconstructed mathematical formulae of Whitehead's theory in Einstein's terminology to make them accessible to contemporary physicists. Synge also treated the problem of a continuous static model, and calculated the gravitational field of a finite sphere of uniform density at rest on the basis of Whitehead's theory.19 Two years later, this result was extended by Rayner to the case of non-static continuous distributions of matter. Calculating the gravitational field of a finite, uniformly rotating, homogeneous sphere, Rayner examined the perturbing effects of the rotation of the central sphere on the orbits of planetary motion, and got similar results to those obtained by Lens and Thirring applying Einstein's theory to the same problem. Rayner also constructed a cosmological model uniformly expanding with homogeneity and isotropy on the basis of Whitehead's theory.20
Whereas Synge and Rayner proved that Whitehead's theory, in spite of the paradigm-difference, had the same conclusions as Einstein's in various applications, Clark for the first time took up the problem of establishing a crucial experiment between the two. Having discussed on the two-body problem, Clark proved that Whitehead's theory of gravitation involves a secular acceleration of the center of mass, and suggested that Whitehead's theory might be refutable by observing the motions of the centers of mass of double stars.21 The same problem was also discussed by Schild, who showed that Whitehead's theory can be modified in such a way that linear and angular momentum are rigorously conserved, and the center of mass of any isolated system has no secular acceleration. Schild added an interesting remark that Levi-Civita, using Einstein's theory of general relativity, obtained a similar secular acceleration, but that this was later proved to be in an erroneous calculation.22
In the 1960s, the confrontation between gravitational theories and experiments again became a matter of concern for physicists. The rapid progress of technology and astronomy made it possible to test various gravitational theories at an unprecedented levels of accuracy. The number of theories in need of testing having increased, the desire to sift them out systematically was intensified. Pioneered by Dicke and Nordtvedt, the various meta-theoretical frameworks of gravitational theories were propounded. Concerning the principle of equivalence on which Einstein founded the general theory of relativity, we must mention the results of redshift experiments in 1965 on the earth by the use of the Moesbauer effect (recoilless emission and absorption of photons). The accuracy of that observation was about twenty times higher than those previously obtained by astronomical observations. This proved to be a strong support for Einstein who had considered the gravitational redshift one of the most important tests of general relativity. Moreover, it is thought by many physicists today that the result of the gravitational redshift proves the so-called Schiff's conjecture that any theory of gravitation must necessarily be a metric theory.
Inspired by Dicke's ideas, Will energetically grappled with the problem of testing in the 1970s, and presented five criteria by which we can eliminate those theories that disagree with experiment. He laid out the "Parametrized Post-Newtonian" framework (PPN) as a meta-theory in which nine metric parameters. varying from theory to theory, made it possible for him to render the various theories of gravitation commensurable. As for Whitehead's theory, Will admitted it was an elegant theory that had been "a thorn in Einstein's side", but claimed that he had now succeeded in refuting it by geophysical effects, the fifth criterion which he had invented.23
According to Will, Whitehead's theory involves a small anisotropy in the gravitational constant G measured by Cavendish experiments on the earth. As the earth rotates, the anisotropy in G produces "Earth tides", i.e. variations in the acceleration g measured by the gravimeter, which are completely analogous to the tides produced by the moon and the sun. Making use of a simplified model of the galaxy, Will calculated the amplitude of the earth tides on the basis of Whitehead's theory, and got the value,
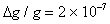
which proved to be 200 times larger than the experimental limit. So he concluded that "Whitehead's theory, after 50 years of life. was "killed" by the geophysical data.24
Will's argument, though accepted by many physicists today as valid, was not without objections concerning the process he used to calculate and estimate the predicted value of earth tides. Fowler claimed that he could reduce the value by a factor of 100 under a different model of the galaxy, and thereby diminish the discrepancy between Whitehead's theory and the geophysical data. Remembering that Whitehead was prepared to adjust his own formulae to take account of new data, Fowler concluded that:
"The real issues between Einstein and Whitehead are not physical but
philosophical. No empirical test can decide the issue of the adequacy of
Whitehead's basic theory of relativity. This issue must be settled on other
grounds."25