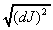and the potential electro-magnetic impetus as dF, we can integrate the total
impetus realised along the time-like world-line AB as follows:
English homepage Japanese homepage Contents
The mathematical formulation of Whitehead's theory is, as in Einstein's case, supplied with tensor-analysis. But it is to the physical structure of gravitational field and not to the geometrical metric of space-time, that the Riemanian theory of differentiable manifold with variable curvature is applied in Whitehead's theory Adopting a different interpretation from Einstein's theory which identifies the gravitational and metric fields, Whitehead introduces the concept of impetus as a physical quantity in order to determine the path of light or of a moving particle in the physical field. There are two kinds of impetus: the potential mass impetus and the potential electro-magnetic impetus.
Writing the potential mass impetus as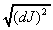
and the potential electro-magnetic impetus as dF, we can integrate the total
impetus realised along the time-like world-line AB as follows:
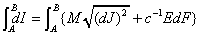
where M is the proper mass as an "adjective" uniformly qualifying the world-line AB,
E is the charge of the mass, c is the velocity of light.12
The two kinds of impetus can be expressed in covariant tensors respectively with first and with second orders, as follows:
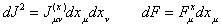
The potential mass impetus is split up into the
difference of two symmetric covariant tensors,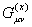 
and
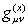: the former represents the inertial
aspect of motion, and the latter the gravitational aspect of the physical field.
Thus we get
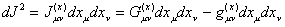
In order to derive the equations of motion Whitehead applies the variational principle
to the above impetus
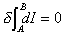
and gets a set of differential equations of the Euler-Lagrange type:
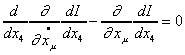
The procedure is mathematically similar to Einstein's use of the variational principle but the meanings of mathematical formula are different: Whitehead separates the physical (contingent) component from the geometrical (uniform) one in what Einstein interprets as a space-time interval. When the effects of gravitation and electro-magnetic fields are negligible, we can derive from Whitehead's equations, as from Einstein's, the law of motion
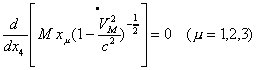
which is nothing but the law of inertia in the special theory of relativity. In the presence of electro-magnetic fields, we get the equations
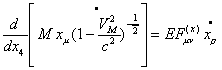
If we identify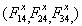 
with the electric force and 
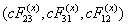with the
magnetic force, the above formulas again agree with those of special relativity.
To sum up, as far as the mathematical syntax is concerned, Whitehead's equation of motion can be regarded as a generalization of the special theory of relativity. It is in the theory of gravitation that the difference between Whitehead and Einstein appears sharply on the level of mathematical formulation, to say nothing of physical interpretation. Whitehead treats the gravitational field on a par with other physical fields, as independent of the metric structure of Mincowski's space-time. Therefore, it is required in Whitehead's theory that the system of n mass particles with gravitational interactions should be mathematically similar to the system of n charges moving under their mutual electro-magnetic interaction. Whitehead's theory of gravitation is sometimes referred as "a theory involving action at a distance with the critical velocity c". This characterization of Whitehead's theory is due to Synge, who located Whitehead's theory between the two extremes of Newtonian theory on the one hand and the general theory of relativity on the other. Such a middle-way character comes from the peculiar definition of the physical field in Whitehead's theory. The physical field of an event P modified with mass m is defined as the domain of P's causal future, i.e. the set of world-lines along which the physical signals propagate from P with the critical velocity c. The distance between P and any event X which is under the causal influence of this physical field vanishes into zero in the Mincowski metric. Thus the causal efficacy may be characterized by an action at a distance propagating with c.
To recast Newton's formula of gravitational potential into a Lorentz-invariant form, Whitehead uses the formula
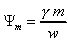
where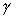 
is the
gravitational constant, and w is a Lorentz-invariant quantity which play the
role of distance from P to the time-like worldline uniformly qualified by the
mass m. The Lorentz-invariant w can be expressed as the inner product of vector
PX and the tangent vector of the world line as follows:
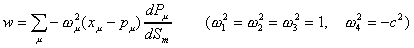
Using the spatial distance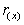 
and the term 
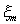depending on the
velocity of the mass, we may also rewrite the above formula as follows:
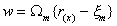
where
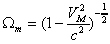
and
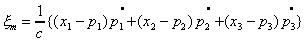
If the mass is at rest, then w becomes identical with the spatial distance r, and we get the Newtonian formula of gravitational potential. Thus Whitehead's theory can give Newton's formula under the special condition. Whitehead's law of gravitation then takes a simple and elegant form as follows:
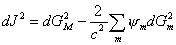
where dJ is the potential mass impetus of an event X, dGM is the invariant differential of the world-line which passes through X modified with the proper mass M, and dGm is that with proper mass m which exerts causal influence on X.13
If we want to find the components of the tensor gu" which represent the gravitational field, we can get them after necessary calculations as follows:14
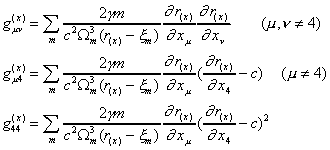
The above equations should not be confused with Synge's reformulation of Whitehead's theory:
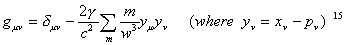
As this formula is easy to handle, physicists usually
mentions it as if it were Whitehead's own. But we must notice that Synge treats
the gravitational field on a par with the metric field in Einstein's manner, and
the notation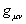 
has a different meaning
from Whitehead's original formula.