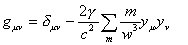
English homepage Japanese homepage Contents
In the previous section we have summarized chronologically the various opinions of physicists concerning the experimental tests of Whitehead's theory as compared with Einstein's. Taking these accounts into considerations, I will try to make clear the meanings of new experimental situations available today so that Whitehead's theory may be reexamined and modified within this context.
First, we should bear in mind the fact that Whitehead's theory contains two levels of arguments. One is propounded as a physical hypothesis, open to the future refutation, and the other is his philosophy of nature which is the guiding principle of his physical theories. For example, his basic equation of gravitation such as
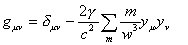
is a refutable hypothesis which Whitehead was able to abandon without altering his background philosophy. In a similar way we can consider it as a hypothesis, and not an inescapable result of his philosophy, to state that "the gravitational forces are propagated along straight lines in Mincowski's space, whereas electromagnetic waves are deflected by the contingencies of the universe," though it is a natural interpretation of Whitehead's formulae. So in one sense it was understandable that Fowler would conclude his remark on Will's alleged refutation by stressing the paradigm-difference.
The present author, however, believes that it is not productive, and is even sterile, to insist too much on the paradigm-priority over observed data. Even today it is logically possible that we believe in the Ptolemaic theory by postulating peripheral hypotheses in order to explain the planetary motion. But physics needs more than logical consistency. We had better consider the refutability of a physical theory on its merit. We always learn something at the time of refutation of our pet-theories.
Take, for example, the thesis that space-time must be "fiat". This thesis was the guiding principle of Whitehead's formulae for gravitation. He admitted openly that he was very willingly to believe that each permanent space is either uniformly elliptic or uniformly hyperbolic, "if any observations are more simply explained by such a hypothesis." But the postulate that the curvature of space-time must be constant was thought by Whitehead to be essential to any satisfactory theory of space-time. It was not a hypothesis, but one of the fundamental principles of Whitehead's theory. I will try to show that the very postulate that the metric structure of space-time must be uniform should be abandoned if we want to learn seriously from experiments which are available today, but were unknown to Whitehead.
We will confine the discussion to the effects of redshift experiments on Whitehead's theory. This does not mean that the problem situations raised by Clark and Will may well be ignored. On the contrary, they should be considered as very important contributions even if there remain some ambiguities concerning their results. Lengthy discussions and mathematical technicalities are involved, if we are to grapple with the problern of earth tides or of conservation laws. Moreover if we abolish the thesis of a uniform metric, we need not insist, as Whitehead did, on the global inertial system, which was responsible for the earth tides in Will's criticism. So it is justifiable first to discuss the problem of the metric structure of space-time.
Einstein, as was pointed out in the first section of this paper, stressed the importance of the gravitational redshifts so much that he dared to say that he would abandon the general theory of relativity if it was not observed. The result, however, of astronomical observations by Freundlich (1930) and others were not satisfactory because of an inaccuracy of measurement. This was one of the reasons why many physicists thought the experimental evidence for the general theory of relativity was not convincing. The situation, however, has changed since 1965, because the aforementioned experiment by the use of the Moesbauer effect gave strong support to Einstein's prediction Since this result is interpreted as verifying the principle of equivalence, some kind of reformulation of Whitehead's theory is necessitated because Whitehead did not accept the principle of equivalence in his original formulations.
Whitehead's theory in its original version (1922), using a simplified model of a radiating atom obtained a gravitational redshift slightly different from that of Einstein's theory by the factor of 7/6. Whitehead also predicted that the values of redshift would depend on the directions of emitted light (Limb Effect), which, at least qualitatively, corresponded to the data of astronomical observation. So it seemed as if the predictive power of Whitehead's theory were equivalent to Einstein's concerning the redshift phenomena, but in fact such an equivalence does not hold. First we must notice the difference of physical interpretations when both theories derive the gravitational redshift. Whereas Whitehead's theory needs additional hypotheses concerning the structure of atomic clock and the nature of interaction between a gravitational field and other force fields, Einstein's theory does not need such auxiliary hypotheses, because the latter postulated that the gravitational fields should directly influence the metric of space-time. One of the most important results of this difference is that whereas Einstein's theory should predict the uniformity of gravitational redshift independently of physical conditions, Whitehead's theory can not expect such a uniformity. This mean that Einstein's theory has a stronger structure than Whitehead's because it runs the risk of being refuted by possible varieties of gravitational redshift. But since Einstein's prediction of redshift has been corroborated by empirical tests since 1965, it gains the advantage of Whitehead's theory because of its completeness.
Moreover there is a further argument against Whitehead's type of gravitational theory as suggested by Schild.26 According to this argument, we must abandon the presupposition of "flat" space, if we accept the uniform occurrence of the gravitational redshift. The argument is as follows:
Suppose that a light signal with the frequency v' is emitted at the
gravitational potential V, and it is observed as a light with the frequency v at
the potential 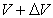 .
.
As the light loses energy during the movement against the gravitational field, becomes smaller than ' according to the equation:
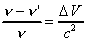
This is the formula for the gravitational redshift. If we consider the light as a wave movement then the above formula involves an apparent contradiction, for it is unreasonable that
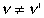
since wave crests cannot originate or disappear between sender and receiver.
This contradiction is resolved by assuming that time flows at different rates at
different levels in a gravitational field. If a clock resting at level V
measures a time interval s' for n oscillations of the wave and if a clock
resting at level 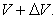 measures a
time-interval s for n oscillations, then
measures a
time-interval s for n oscillations, then
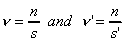
Substituting this into the aforementioned formula, we get:
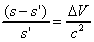
This is the formula for the gravitational time dilatation.
If we presuppose that space-time is fiat, we find that it is contradictory to
the above result of time dilatation. In Minkowski's space-time, the world-lines
of two clocks at rest are parallel to the time-axis. Suppose that the stationary
gravitational field is parallel to x-axis, and the light signal, emitted from
the world-point P with the potential V, is received at the world-point Q with
the potential 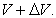
After the time-interval s', measured along the lower world-line of the clock
at the potential V, another light signal with the same frequency is emitted from
the world-point Q, and received at B which lies at the higher world-line of the
clock at the potential 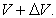
As the whole setup is stationary, PA and QB are parallel to each other, and PABQ must be a parallelogram. Therefore PQ(s') must be equal to AB(s), which is contradictory to the formula for the gravitational time dilatation. Simple as it is, the above argument shows clearly that the Whiteheadian theory of gravitation needs some modifications in order to explain the uniformity of the gravitational redshift. Of course we can escape form this difficulty simply by postulating as an auxiliary hypothesis that the gravitational field exerts a physical infiuence uniformly on the inner structures of atomic clocks. But such an ad hoc remedy only shows that we had better adopt Einstein's thesis that the gravitational field directly affects the space-time metric. The only alternative is to take what Whitehead called "potential mass impetus", dJ, as measuring the element of proper time along time-like world-lines. This type of modification, as Synge and others showed, makes it possible to deduce the uniform redshift from Whitehead's equations. We can get the same predicted value of redshift as that of Einstein's equations.
But we must bear in mind that the above remedy requires us to reformulate one of the fundamental tenets in Whitehead's theory, i.e., that space-time should have the uniform structure independent of matter. Accepting the influence of gravitation on metrical properties of space-time, we are obliged to ask the following question. To what extent may we admit the effects of matter on space-time and at the same time remain faithful to Whitehead's philosophy of nature?
As was stated in the second section of this paper, Whitehead rejected the priority of matter over space-time. In his philosophy of nature, events are ontologically prior to matter and space-time. Matter is treated as an "adjective" of events, and cannot influence the essential properties of space-time which should be decided only by the interrelated structures of events. The existence of matter only affects the accidental attributes of space-time. So there are two alternatives concerning the status of metric properties. One is what Whitehead adopted in his formulation of physical theory: the metrical properties of space-time are independent of matter. But this choice is untenable if we take seriously the aforementioned results of experiments. So we must take the other alternative. i.e. the metrical properties of space-time are indeed affected by the existence of matter, but the topological properties are independent of matter. It must be noticed that Whitehead himself was absorbed in the topology of events as the "theory of extensive continuum" in his later philosophy of nature.27 For example, he tried to define the concept of "straightness" or "flatness" without relying on any metrical property, but only through the interrelated structures of extended regions. So the idea of topology without metric as the determinant of space-time may be called Whiteheadian, though it is not explicitly stated in The Principle of Relativity where he stresses the uniformity of metrical structure.
If we adopt the idea of the topological priority of events over matter, we
can restrict the extent to which the distribution of matter exerts influence on
the topology of space-time. On the other hand, if we think that the structure of
space-time totally depends on the distribution of matter, we are confronted with
a queer situation, which Goedel called "the Ideality of Time" in one of the
solutions of Einstein's equation;28 i.e. Einstein's theory is consistent with
the cosmological model where "for every possible definition of a world time one
could travel into regions of the universe which are passed according to that
definition." Einstein himself admitted in his response to Goedel that the
directionality of time cannot be determined within the framework of general
relativity, for the topological structure of the universe might be determined by
matter in such a way that the time-like world-line is found to be closed.29 As
Whitehead's philosophy of nature insists on "the reality of time", i.e., the
reality of events which cannot be repeated, it would be productive for the
future development that a new version of Whiteheadian theory of relativity
adopts the idea of topological priority of events over matter, instead of the
uniformity of a space-time metric .